大学入試の数学の良問を出題大学別に徹底比較！

大学入試の数学の攻略は良問を解くことから！

　大学入試の数学では難しい大学ほど難しい問題を出す、というのが一般常識です。ですがそれだけではなく、実際には大学によって出題の傾向、つまり問題の出し方が異なってきます。このため、基本的には志望する大学の過去問を何年分も遡って解いて出題のクセを見抜き、それに見合った対策をしていくことになります。

　しかし、それだけで大丈夫でしょうか？各大学の出題の特徴は他の大学の出題と比較して初めて際立つものです。ですから、今までの出題傾向に合わせた勉強ばかりしていると、傾向が変わった時に「こんな問題解いたことない！」と試験本番でパニックになり、残念な結果に終わってしまいます。

　そんなことは起こらないだろう、と思われるかもしれません。ですが大学入試はその後の人生を左右する大事な試験です。その時の出題者の気まぐれでその先の進路が変わってしまってはたまりません。ですから、本来するべき数学の勉強はどんな問題が出ても解けるよう、基礎を完璧にし、ありとあらゆるタイプの問題を解くことです。過去問演習はそれが出来てから行うものです。

　しかしながら、それでやみくもに問題を解いていくと時間が足りなくなります。また、入試問題にも良し悪しがあり、問題によっては数学の力がかえって鈍ってしまう恐れもあります。逆に言えば、精選された良問を解くことこそが、大学入試で通用する数学の力を身につける一番の近道なのです。

　このページでは難関大学入試に挑む受験生、数学の力を伸ばしたい高校生に特に解いて欲しい、3つの大学の問題を計9問ピックアップしています。大学ごとに問題をまとめ、ポイントを紹介しています。各問題の画像をクリックすると、その問題の詳細な解説や、解法に至るまでの考える道筋を見ることができます。ぜひ、ページの隅から隅までご覧ください。

各大学の数学の良問9選

東京大学の出題の特徴と3つの良問

　日本の最難関大学である東京大学の問題には、東大の出題者が考える「入試問題はこうあるべき」が詰まっています。それは時折、入試問題を通した教育現場への、そして社会全体へのメッセージとして現れます。

　では一体、東大の出題者は入試問題はどうあるべきと考えているのでしょうか？答えは単純で、「その人の本当の実力が現れる問題であるべき」というのが彼らの考えです。そのため、まず最初に行われるのが「丸暗記の排除」です。パターン学習で大学入試に特化した勉強ばかりをしてきた生徒を落とし、真に卓越した実力者を迎えられるように入試問題を作成することが彼らの目標になります。そして、その方針のもとで作られる東大の入試問題は、すべて教科書の勉強だけで解けるようにできています。

　…しかし、これは理論上の話です。実際に教科書の勉強だけで東大に入れる人は毎年、全入学者の1割もいません。ですが、所謂教科書の勉強の肝は「公式や定理を考えなしに暗記せず、全て自らの手で証明を書けるぐらい理解してから使うこと」にあります。これが東大の、いや、大学入試の数学を解く上で最も重要になります。

　ここで紹介する3問はこの「公式や定理をしっかり理解する」ことが特に重要になる3問です。

①ゆとり教育への挑戦状？

 

　恐らく大学入試史上最も有名なこの問題。当時「詰め込み教育」へのバッシングなどからゆとり教育の導入が進みましたが、1999年秋に「2002年から小学校の教科書で円周率が3になる！」という誤解が広まり、この問題が出題される頃には「円周率は3」というフレーズが社会現象になっていたのでした。

　実際には円周率が3で教えられることはほとんどなかったのですが、本当に円周率が「3」だったならば大変です。半径1の円に内接する正六角形の周の長さは6です。しかし、外接円の円周を3という円周率で計算すると、なんとこちらも6という信じられない結果になってしまいます。

　社会に対するメッセージ性や、理論上は中学生でも解けてしまうほど簡単な問題であったため、マスコミでも大きな話題になりました。しかし、本当にそう上手くいくでしょうか？ぜひ解いてみて、こちらから確かめてみてください。

②公式は証明してから使おう

 

　この式は数学Ⅱの教科書には必ず載っている、おなじみ三角関数の加法定理です。多くの人はこの定理を、色々な覚え方を試して無理やり覚えたものと思われます。

　しかしこれを証明せよというのが東大の目の付け所の凄さです。この公式を用いることで倍角の公式や三角関数の導関数の導出など、様々な操作が出来るのですが、肝心の加法定理は証明せずにスルー、という受験生が後を絶ちませんでした。そんな状況下でのこの出題です。

　三角関数の定義をいうだけの(1)も含めて、どこの教科書にも解答が載っているという本当に基本的な問題のはずなのに、実際の試験での正答率はわずかに20%程度でした。自分の手で何も見ないで証明できるか、少しでも怪しいなと思ったらこちらをクリックしてください。

③閻魔が笑えば赤門は開く

 

　この問題が出題されたのは今からなんと70年も前のことです。入試業界で「閻魔の唇問題」として有名な一連の問題のうち、最初に出題されたのがこの問題です。当時の正答率は今までに紹介した2問よりもずっと低かったとされています。

　実際にこの問題を解き、解説を読んでこの難しさの理由を確かめて頂きたいです。「なぜ伝説の入試問題と言われ続けるのか？」「どうして他の大学が似たような問題を出し続けているのか？」その理由も、こちらをクリックして頂ければわかるかと思います。

京都大学の出題の特徴と3つの良問

　OB,OGのノーベル賞受賞者数が堂々の日本一であることで有名な京都大学。iPS研究所をはじめ、「研究の大学」として有名な京大ですが、実はこの大学には日本唯一の純粋数学の研究所である「数理解析研究所」が存在し、入試問題も研究所の先生が作っている、と言われています。

　ところで、「京大らしさ」とは何だと思いますか？多くの人は奇抜さとか、浮世離れしたものを思い浮かべるかもしれません。しかし、少なくとも、数学における「京大らしさ」は数学という学問そのものへの真っ直ぐな気持ちであると考えましょう。

　これを反映するのが京大の出題と採点基準です。京大の問題は一見奇抜に見えますが、そのベールさえ剥ぎ取ってしまえば、いたって正統派な問題です。どのような問題も、「こういうことを考えると面白いよ」という出題者による一種の「おさそい」です。

　一方で採点の厳しさは本物です。数学的に少しでもおかしい所があればバッサリ減点されます。特に厳しく言われるのが十分条件と必要条件で、ここをよく分かっていない答案が非常に多く、毎年たくさんの人が大幅に減点されているようです。

　さて、これから紹介する3問は、上に挙げた2点に注目してみてもらいたいと思います。「こういうことを考えてみるのも面白くないだろうか？」という出題者の想いの詰まった問題です。どれもかなり難しいですが、試行錯誤をして答えを出す喜びを是非とも体感して頂きたいと思います。

①自分の得点を自分で決められる？

 

　自分の点を自分で決められる。このような問題は他にはありません。ですが、実はこの一見してとっても優しい問題には実はとんでもない罠が仕掛けられています。

　その理由は実際に解いてみると分かります。(1)よりnは1から6の6通りに出来るので早速それを使ってn=1から試してみると、g(1)=0、この場合は0点です。じゃあn=2とn=3も試してみよう、と思ってやってみたらg(2)でもg(3)でも結果は0点です。これでこの問題の意地悪さが分かるでしょう。

　n=1から真面目に試せばその時点で出題者の掌の上です。ではどうすればよいのか？そう思ったあなたはぜひこちらから確かめてみてください。

②極限と微積にはこの一問！

 

　2番目に紹介するこの問題はたったこれ一題で数学Ⅲの極限と微積を総復習できるスグレモノで、筆者が特に薦める問題です。一見して何がしたいのか分からないような問題にも見えますが、格子点の数を数えるところから地道に始めることで、色々な問題を解くための「道具」の使い方が学べます。

　……ですが数学には別解がつきものです。極限の計算は回避できないですが、しばしば煩雑になる微積の計算を回避する解き方もあります。そしてその解き方は賢い人ならすぐに察しが付くとはいえ衝撃的な「裏ワザ」です。この「裏ワザ」が気になる人もそうでない人も、数Ⅲを攻略したい、という人はぜひ上の画像をクリックしてください。

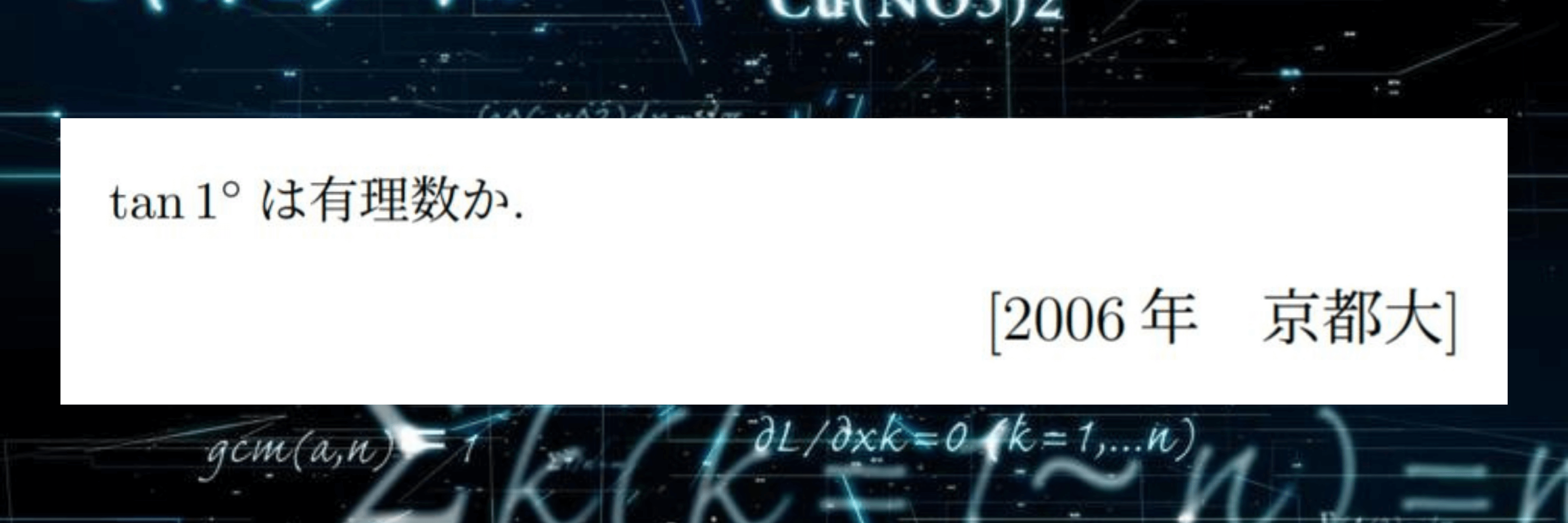
③史上”最短”の入試問題

 

　京大の数学を語る上で避けては通れないのがこの問題です。「たったこれだけで入試問題になるの？」と思った方もいるかもしれませんが、なります。とはいえ、実際の試験では見当をつけられずに敬遠した受験生も多かったようです。

　しかし、ここで問われていることはごくごく基本的なもの。どこから攻めたらよいかを問題文から読み取るのもまた数学の能力です。この問題はこの読み取りが非常に重要な出題です。日本の大学入試史上最短のこの一題、ぜひ上のバナーをクリックし、実際に解いてみてください。

東京工業大学（現：東京科学大学）の出題の特徴と3つの良問

　東京工業大学は日本の工業大学の中でもダントツの教育力と研究力、そして医科ではない単科大としてかなり高い入学難易度を誇ります。入学が難しい最大の理由は高すぎる数学の難易度にある、といわれています。東工大の数学は180分という京都大の理科に並ぶ日本一長い試験時間をとっており、体力的に厳しい上、問題の出題方法が他大と比べて特徴的です。

　例えば、以下のような問題が出題されたことがあります。

　この問題は当時そのまま採点してしまえば「平均点0点」になってしまい、東工大の採点者が対応に追われた逸話があることで有名な非常に難しい問題です。ここで詳細な解説はしませんが、nを見かけたらまず帰納法です。ですがこの場合、果たして帰納法を使うべきはnとkのどちらに対してとなるでしょうか？

　ここでの答えは「nにもkにも使わない」です。この問題はP(x)が多項式で与えられるので、これが整式である、すなわち全ての係数が整数であることを示すことになります。そのため、nよりも小さい全ての整数mに対する多項式をつくり、それが仮定のもとですべて整式になることを示すことになります。

　このように、問題文の指示を把握することすら難しいのが東工大の出題の特徴です。それだけでなく実際に解答を作る作業すらも難しいことから「東工大の数学は日本一難しい」と言われることも多いです。

　ですが、出題が難しい分受験生の力量を試す問題としての質は高く、ここから引用できる良問も多いです。今回はその一部を紹介していきます。

①答えはすぐに分かるけれど

 

　素数を扱う問題で、しかも19のn乗が問題文に登場するという見た目からして難しい問題です。とりあえずnが出てくる問題は具体的に数え上げるのがセオリーなので、n=1から順番に代入します。すると、a_1=21、a_2=329がすぐに分かり、この2数を割り切る素数は7しかないこともすぐに分かります。

　ですが、この結果だけを見て「答えは7」などと書こうものなら0点です。問題文には「a_nのすべてを割り切る」とはっきり書いてあります。ですから、nが3以上の場合でもa_nは7で割り切れることを確かめなければなりません。

　そうすると、この問題は「すべてのnに対して、a_nが7で割り切れることを証明する問題」であると読み替えることができます。しかし、このように読み替えることができても難しいのが東工大の数学です。皆さんも実際に手を動かしてこの問いにぶつかってみて、きちんと証明できたか、こちらの問題解説から確かめてみましょう。

②複素数平面、基本のキ

 

　ここでは数学Ⅲの「複素数平面」から、解いていて非常に爽快感のある良問をピックアップします。こちらは複素数平面のなかではとても基本的な問題なのですが、この分野は覚えることが多く、習ったことの一つ一つが頭の中ではっきりしていないと手も足も出なくなります。だからこそ、東工大でも十分入試問題になるのです。

　まずは解が3つですから、それらをα,β,γのようにおきましょう。その次にすることはなんですか？……そうです。複素数αが解ならそれに共役な複素数も解であることを利用するのです。このようなことが頭の中でポンポン出てくる段階になるまで勉強できていれば、この問題はパズル感覚で解けます。

　複素数平面に自信がある人は頭の体操として、苦手意識のある人は苦手を克服するために挑戦してみましょう。まずは上の画像をクリックしてみてください。

③いびつなサイコロ

　※難問注意！！

　　確率の勉強中に誰しもが「同様に確からしいサイコロなんて本当にあるの？」と思ったことがあるかと思います。その通りです、サイコロは工場で作る段階でバラツキがありますから、お店でたまたま買ったサイコロが1から6までそれぞれ誤差なく1/6で確率を出してくれる、ということはそうそうないでしょう。

　この問題はそんな身近にありふれた「いびつなサイコロ」を取り扱っています。つまり、市販の六面ダイスの性質を考察する問題です。ですがこんな身近な題材であっても、「確率が等しくない」という理由だけで数学者ですら頭を悩ます難問に大化けします。この問題も、多くの受験生が手も足も出なかった難問中の難問です。

　ですが、この問題の素晴らしい所は工夫次第で発展的な内容を回避して答えが出せる、という点です。本番でこの問題が出れば思わず手が止まってしまいますが、練習の段階では怯まずぶつかる価値のある良問です。一体どう考えればいいのか、詳しいことは上の画像をクリックしてみましょう。

実際に本番の問題が
解けるようになるには？

　ここまでの問題はどうだったでしょうか？かなり有名な問題も取り扱ったので、もう何題か解いたことあるよという人もいるでしょうし、このレベルの難問に当たったことがほぼなくて、どれも難しいという人もいるでしょう。ここからは実際に本番の問題が解けるようになるために必要なことを解説します。

　大学入試の数学は事前準備が7割です。残りの3割は本番でのメンタルと健康管理の話なので、ここではそれについてはあまり触れません。とはいえ本番で何をやったらいいかわからないようでは困ります。なので、ここでは事前に準備するべき要素について本番に繋がる形で解説します。

　まずは「難易を見切る力」をつけることです。難しい問題はほとんどの人が手をつけずに終わる一方、簡単な問題は誰でも解いていきます。ですが、入試本番でどの問題が簡単でどの問題が難しいかも分からずに解き進めると、難問で時間を浪費して簡単な問題を解けずに不合格、ということが起こり得ます。

　次に「解答の書き方を身につける」ことです。数学には数学の作法があります。これを身につけているかいないかで大きく点差が開きます。伝えるべきことだけを採点者に伝えられるようにするテクニックは大学に進んで学問をやるにしても、その後就職して仕事をするにしても必要な技能です。

　そして最後に「計算力をつける」ことが最も重要な準備になります。数学の問題を解くなら当たり前のことですが、計算ミスでその後の人生設計が大幅に狂うことだってあり得ます。ですから、日頃から計算練習を積んでおくに越したことはないのです。

　では次に上に挙げた3点をいかにして身につけるかについてです。実は上記3つの準備は自力でできます。ですがそれは理論上の話。どれをとっても膨大な時間が必要ですし、特に真ん中の「解答の書き方を身につける」に関して言えば、それを自力で身につけることがそもそも難しい人だっているはずです。

　そこで、そうした準備のために足りない部分を補ってくれる優秀なサポーターとして、私達東大家庭教師友の会に所属する家庭教師をご提案します。彼らはみな大学入試を経験した現役の学生家庭教師であり、上記3点の準備をするために最も効率のよいやり方だけでなく、今回取り上げたような良い問題の選び方まで熟知しています。

　ここからは当会所属の家庭教師だからできることを紹介していきます。大学入試の数学を攻略したい、第一志望校に合格したいというあなたの背中を、私達は全力で押します。