今回の問題を解くために
必要な道具
この問題は普通に解けば、数学Ⅲ・数学Cまでの範囲内のいわゆる「理系数学」の問題を解くうえで重要な知識をいくつか身に着けることができます。それぞれ、おおよそ以下の通りです。
格子点

\((x,y)\) 座標がともに整数になる座標平面上の点のことを格子点といいます。上の図は \(y\leq n-x\) かつ \(x\geq0\) かつ \(y\geq0\) の範囲の格子点の一部を表しています。ではここで問題です。この範囲で格子点はいくつになるでしょうか?
格子点問題の解答方針の基本は「 \(x\) 座標を固定して数え上げ」です。具体的には直線 \(x=k\) (kは整数)上に存在する格子点の数を数えて、それを0からnまでの範囲で足し合わせる作業が必要となります。

上の画像から分かるように、直線 \(x=k\) 上に存在する条件を満たす格子点の数は \(n-k+1\) 個となります。あとはこれを \(k=0\) から \(k=n\) まで足し合わせましょう。これにより、求める格子点の数は$$\sum_{k=0}^{n}(n-k+1)=n(n+1)-\frac{n(n+1)}{2}+n+1=\frac{(n+1)(n+2)}{2}$$となります。
余談ですが、ここで紹介した格子点は「格子」とよばれる数学上の概念のごく一部に過ぎません。この概念を理解するためには大学レベルの数学の知識が必須となります。
はさみうちの原理
はさみうちの原理の主張は数列 \(\{a_n\}\) と数列 \(\{b_n\}\) が \(n\rightarrow\infty\) で両方Aに収束するならば、この2つの数列に挟まれた数列 \(\{c_n\}\) もAに収束する、というものです。高校の段階での証明はできないので、使用する際は必ず「定理」ではなく「原理」と書いてください。
大学入試の数学において、多くの極限の問題はこの「はさみうちの原理」を用いて解くことになります。練習も兼ねて、ここで一つ数学的に重要な事実の証明をしてみましょう。$$問題:r<1のとき、\lim_{n\rightarrow\infty}r^n=0を示せ。$$ これは数学Ⅲの極限のかなり早い段階で教わる事実ですが、皆さんはきちんと証明できるでしょうか?方針として、このままだとやりづらいのでまずは \(s=1/r\) としましょう。こうすると、 \(s>1\) を用いて証明ができます。

このように二項定理を用いることでこの事実を証明することができます。「0が0に収束する」という言い回しは国語的にはおかしいかもしれませんが、これは2つの不等号の外側の式が \(n\rightarrow\infty\) で0に収束する、という解答根拠を明確にするためのものです。
はさみうちの原理を利用する問題は多くの場合、示したいものをはさむ2つの数式を見つけることが難しいです。一応、上の例のように片方を定数にすることで1つ見つけるだけでよくするテクニックも使えます。ただし、これも時と場合によります。
区分求積法
こちらは高校数学の極限の問題における「最後の大物」です。大学入試の数学では極限の問題を解くためのパターンが「はさみうちの原理」「ネイピア数eの定義」「sinx/x→1」の3通りありますが、それらのどれでも解けない問題に対してはこの区分求積法が輝きます。
区分求積法は \(0\leq x \leq1\) で連続な関数 \(y=f(x)\) に対して、$$\lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}f\bigg(\frac{k}{n}\bigg)=\int^1_0f(x)dx$$が成り立つことを利用して、極限を積分計算によって求める、というものです。一見して何が起こっているのかよくわからないような式ですが、図形的には以下のようなものとして理解できます。
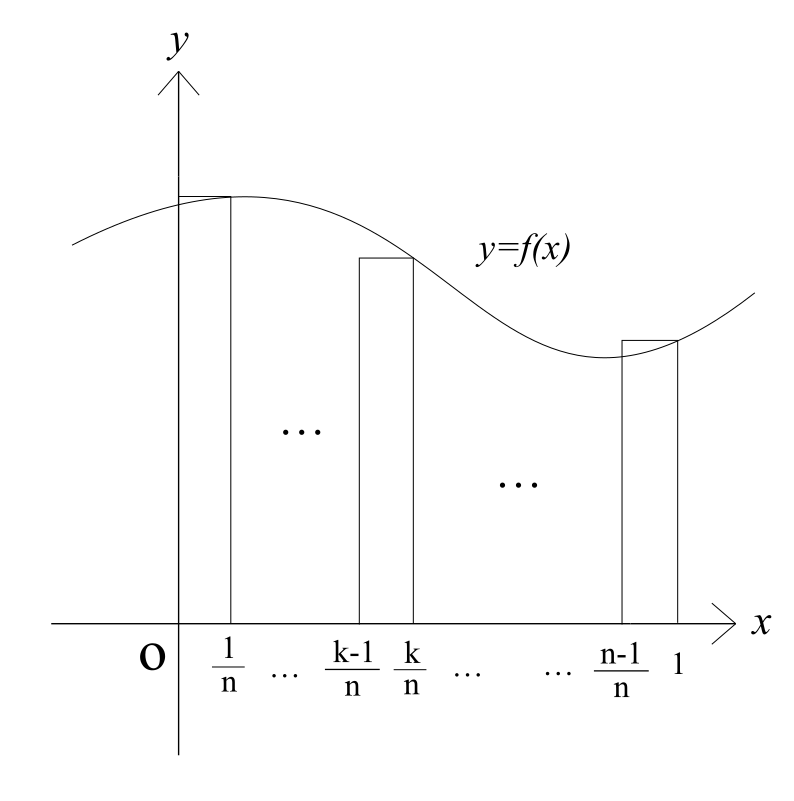
まずは0から1までをn分割します。すると、この図において \(\frac{k-1}{n}\) から \(\frac{k}{n}\) までの区間の棒グラフになっている部分の面積は、図より \(f(k/n)\) をnで割ったものである、と解釈できます。これをk=1からk=nまで足し合わせれば \(y=f(x), x=0, x=1, y=0\) で挟まれた部分の面積とだいたい一緒になる、ということが区分求積法の考え方です。 \(n\) を無限に大きくすることでより両者の面積は等しくなっていくことも直観的にわかるでしょう。
実は、理論的には私達がよく知る不定積分の前に、このような区分求積法の考え方を用いた定積分があります。これを出発する積分体系をリーマン積分といいます。理系の人は大学に進んだ最初の年に必ず、この積分体系を理論的に学習することになります。
今回の問題を解くために
必要な考え方
一通りの道具の説明を終えましたので、ここからは問題の解き方を考えていきます。まずは以下の図をご覧ください。
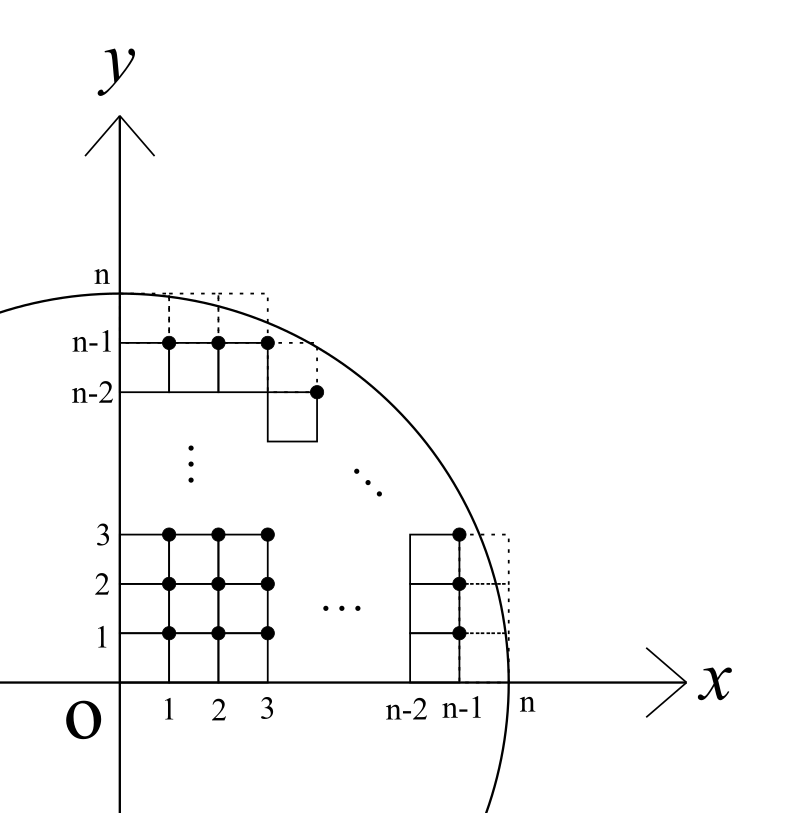
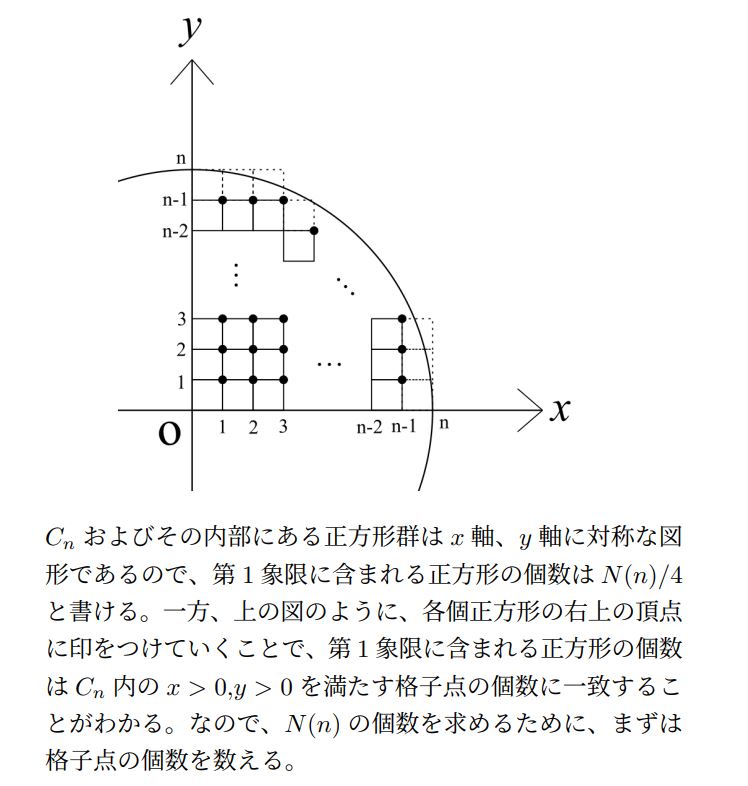
問題文にある \(C_n\) に含まれる面積1の正方形を第1象限について指示通りに敷き詰めるとこのようになります。すると、第1象限では正方形の右上の点が格子点になって、これがこの範囲での正方形の数に一致する、だから今回の問題は格子点の問題に読み替えられる、と気付くことができます。
同じことが第2、第3、そして第4象限に対しても成立します。すると、対称性から第1象限に存在する \(C_n\) に含まれる格子点の数は \(N(n)/4\) になることに気付きます。あとはこの格子点を数え上げるだけです。
……とはいえ、この格子点の数え上げもちょっと一工夫する必要があります。例えば、直線 \(x=k\) 上かつ第1象限上にある \(C_n\) に含まれる格子点を考えようとしても、上の図を見れば「 \(C_n\) は円だからそこにいくつの格子点があるかすぐわからない」ことに容易に気付くはずです。
このようなときに役に立つのが「ガウス記号」とよばれる記号です。高校では[]がガウス記号に相当し、例えば \([x]\) は「 \(x\) 以下の最大の整数」を表します。格子点の座標はどちらも整数なので、これが使えそうですね。具体的にどう使うのか、これから解答を見て確かめていきましょう。
解答
解答は以下のようになります。





ガウス記号によって \(N(n)\) をはさむ不等式をつくって \(n^2\) で割って答えが出そうな形に持っていく、ここまでは前段の発想法の解説を読めば辿り着けると思います。しかし、その後の極限の導出で区分求積法を使う、これは慣れていないと発想しにくいです。
大学入試の数学では基本的に「極限の問題で \(\frac{k}{n}\) を見たら区分求積法」です。こればかりは慣れがないとどうしようもありません。はさみうちの原理を使うシナリオが見えるかどうかも含めて、日頃から数学Ⅲの問題演習をしっかり積んでいるかがそのまま反映される問題である、といえそうです。
30秒で満点が取れる
衝撃的な別解
正攻法での解答を見て頂いたところでここからは裏技紹介のお時間です。今回の問題は以下のようにすれば1分もかけずに完答できます。

これで満点です。数学的に間違っている箇所はどこにもありません。 \(n\) が \(C_n\) の半径であることに注目して、「正方形の面積の総和とCnの面積はほとんど一緒ではないか?」というような発想ができれば作れなくもない解答ですが、これをひねり出すのはかなり難しいです。
「逆にこの発想の方が普通ではないか?」と言う人もいるかもしれません。しかし、少なくとも本番ではこのような裏技ではなく正攻法で戦えるようにするべきです。そのためには確かな知識をつけ、しっかりと演習を積むことを普段から意識するべきでしょう。
大学入試の数学Ⅲの問題を
解けるようにするために
今回は数学Ⅲの問題を解くために必要な「極限」「微積」のうち、「はさみうちの原理」と「区分求積法」に着目した問題を解いていただきました。しかし、数学Ⅲの極限と微積にはまだまだ重要な概念が残っています。その一部を紹介します。
ネイピア数eの定義
ネイピア数、あるいは自然対数の底として知られる \(e\) は以下のように定義されます。$$\lim_{x\rightarrow0}(1+x)^\frac{1}{x}$$ これについては \(y=a^x\) を微分して得られる導関数 \(y’\) も \(a^x\) となるようにできる \(a\) の値を見つけ出す方法で証明をすることができますが、長いので今回は省略します。逆バージョンとして、$$\lim_{n\rightarrow\infty}\bigg(1+\frac{1}{n}\bigg)^n$$も記憶しておきましょう。 \(x\) の右肩に \(1/x\) が乗っているような式を見たら、「これを用いるべきでは?」と発想できるよう、日頃から問題演習を積んでおくべきです。
平均値の定理
平均値の定理とは、ある関数 \(y=f(x)\) が \([a,b]\) で連続かつ \((a,b)\) で微分可能であるときに、$$\frac{f(b)-f(a)}{b-a}=f'(c) かつ a<c<b$$を満たすcが最低1つは必ず存在することを示す定理です。「ナニコレ?」と思われた方のために画像を用意しました。おおよそ以下のようなことを指しています。

例として、 \(y=f(x)\) の概形を上のように与えます。x=aからx=bまでの傾きを示す直線は図中の青線で与えられます。これに傾きが等しい赤色の接線が最低一本以上、aとbの間で与えられることを示すのがこの定理です。
平均値の定理を使用する機会はかなり多いです。使用上の注意として、平均値の定理の成立には閉区間で連続であることと開区間で微分可能であることが必要です。この2つを確認せずに答案を書き始めると大幅に減点されるので気をつけましょう。
媒介変数と積分
\(x=f(t), y=g(t)\) で表される2つの \(t\) についての関数が与えられます。 \(t\) をある区間でプロットしていくと、多くの場合は1本の曲線が現れます。この媒介変数tについて、数学Ⅲでは大きく分けて2種類の積分問題が存在します。
1つ目は曲線の長さを求める問題です。結論から話すと、 \([a,b]\) の間を動く媒介変数 \(t\) に対して、関数 \(y(t)=f(x(t))\) が描く曲線の長さを \(L\) とすると、$$L=\int_a^b\sqrt{\bigg(\frac{dx}{dt}\bigg)^2+\bigg(\frac{dy}{dt}\bigg)^2}dt$$で与えられます。これがどういうことかは以下の図で解説します。
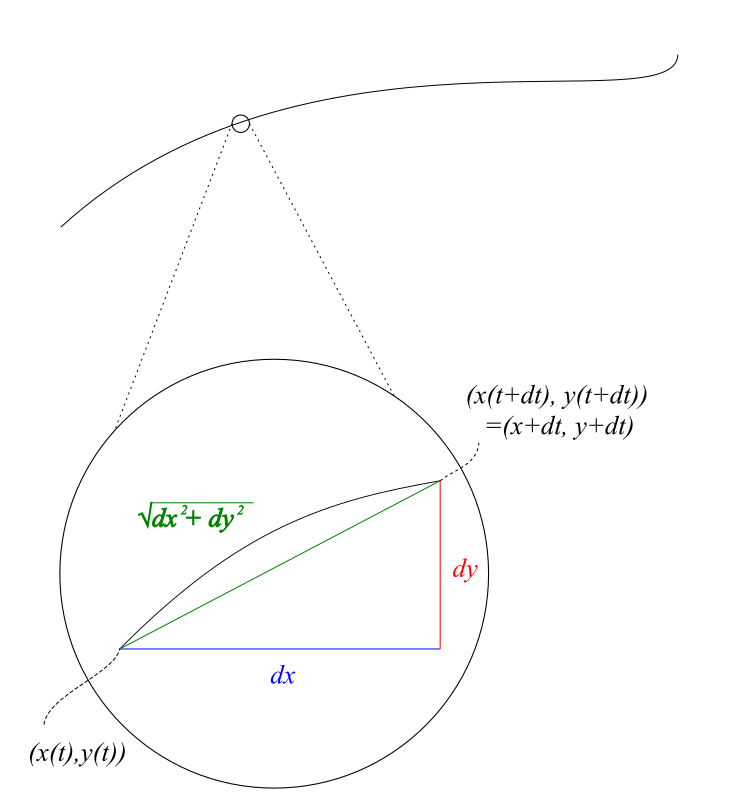
\(t\) が \(dt\) だけ動いた時、 \(x\) は \(dx\) 、 \(y\) は \(dy\) 動きます。すると、その間に曲線が描く距離は$$\sqrt{dx^2+dy^2}$$として近似できます。これを \(t=a\) から \(t=b\) までつなぎ合わせることが先ほどの式の意図です。 \(dt\) を後ろに出すために \(dx^2\) と \(dy^2\) をそれぞれ \(dt^2\) で割ることで完成します。
ちなみに、 \(t\) に対して \(x\) が単調増加する場合(すなわち、 \(x\) と \(y\) が一対一対応する場合)には、先ほどの式を$$\int_a^b\sqrt{1+f'(x)^2}dx$$の形で書くことがあります。
2つ目は極座標で表された関数の積分問題です。極座標は数学Cの範囲ですが、京都大学などの大学では極座標と積分を組み合わせた融合問題が出ることがあります。先ほどの内容が \(x=r\cos\theta, y=r\sin\theta\) に置き換わるだけです。例えばこちらをご覧ください。

こちらも京大の過去問ですが、この問題はそこまで難しくありません。むしろ「解けなかったら落ちる」レベルの問題です。とりあえず \(x=r\cos\theta\) と \(y=r\sin\theta\) の式に \(r=1+\cos\theta\) を代入し、先ほど説明した曲線の長さの話に持ち込めば解けます。京大ではこのような問題は頻出です。
以上のような概念は一朝一夕に身につくものではありません。よほどの天才か要領がいい人でなければ、定着にはかなりの時間を要します。
そもそも大学入試の数学自体、自分で手を動かして身につけなければならない事項は多いです。合格するその日まで、無数に問題を解き、走り抜ける覚悟を持たなければなりません。そして、往々にしてそれをたった一人でやりきることは難しいです。
しかし、助っ人がいるとどうでしょう?わからないところを丁寧に教えてくれるうえ、モチベーションをたくさんくれますし、悩み事があれば相談にも乗ってくれます。このような素敵な助っ人がいれば、大学入試も怖くありません。
私達東大家庭教師友の会はそのような素晴らしい助っ人となれる学生家庭教師を紹介できます。彼らは全員難関大学在籍の家庭教師です。さらに大学受験を突破して日が浅いことから、指導は的確なうえ、生徒様に親身になって接してくれます。
大学入試の数学を攻略したい、第一志望校に合格したいあなたの背中を、私達東大家庭教師友の会は全力で押します。
あわせて読みたい|大学数学の良問を解説!
東大家庭教師友の会の特徴
当会には、東大生約9,700名、早稲田大学生約8,500名、慶應大生約8,000名をはじめ、現役難関大生が在籍しています。
生徒様の憧れとなる教師のご紹介と、安心・充実のサポート体制で、生徒様の目標達成に貢献します。
大学受験数学の指導ができる家庭教師の紹介
上記は在籍教師の一例です。他にも様々な経歴の教師が在籍しています。ご希望の条件の教師が在籍しているかは無料でお探しできますので、まずはお気軽にお問合せください。
オンラインでの指導も可能です
東大家庭教師友の会オンラインHPを見る



















