京大入試の数学の良問その３　～史上”最短”の入試問題～

今回の問題にまつわる
エピソード

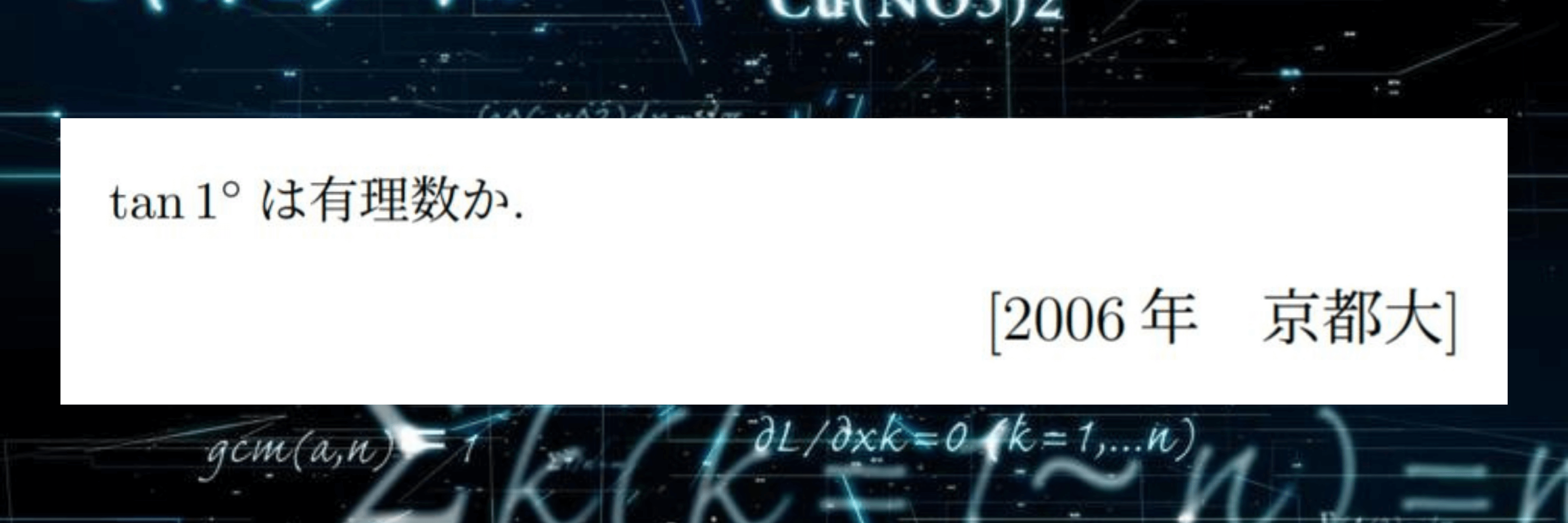
　この問題が出題される3年前に東大で「円周率は3.05より大きいことを証明せよ」という問題が出題され、一時期これが「史上最も短い入試問題」になっていました。それで対抗心を燃やしたのか、京都大学が2006年の後期試験の文理共通問題として出題したのが今回の問題です。

　tan1°をそれぞれ「t」「a」「n」「1」「°」と切り分けて数えても、最後のピリオドを足してもたったの11文字。これだけで大学入試の数学の問題として成立するという、この時点でも良い問題であることは確かですが、解いてみても素晴らしいのがこの問題です。その理由を見ていきましょう。

今回の問題を解くために
必要な考え方

　数学の問題を解くためにまず最初にすることは何でしょうか？もちろん、「問題文を読む」ことです。ですが、今回は問題文にたったこれだけの情報量しかありません。そのため、いつも以上に問題文をしっかりと分析する必要があります。

　じゃあ一体どう読めばいいのでしょうか？まずは問題をいくつかの要素に分解します。まず、「tan1°」「有理数」「か」の3つに分けましょう。

　最初に考えるべきは「か」の部分です。この部分を補って元の問題を読むと、「tan1°は有理数ですか？それとも違いますか？」という意味になるのは明らかです。そのため、「有理数であること」の反対を探すために、次は「有理数」の部分について考えます。

　高校の範囲では複素数までを扱います。複素数の中には実数があり、実数は例外なく有理数と無理数に分けられます。当たり前のことのようですが、tan1°は有理数か無理数のどちらかです。

　こうした二者択一の問題は背理法で処理することになります。あらかじめ「tan1°」が有理数かどうかの見当をつけて、違うと感じた方であると仮定して書き始めることになります。

　これから解答を書きます。まだ答えが出ていない人は、とりあえずどちらかだけ予想してみてください。可能なら手を動かして答案を書いてみましょう。

解答

　解答は以下の通りになります。

　また、帰納法ではなく、倍角の公式を使った方法でも解けます。その方針で作成した解答も以下に掲載します。

 

　どちらの解答でも、tan1°は無理数であるという見切りをつけて、tan1°が有理数だとすれば矛盾が起こることを示すというやり方をとっています。tan30°=1/√3は教科書に載っており、また√3が無理数であることは広く知られる数学的知識なので、省略しても問題はないでしょう。

　ですが、√3が無理数であることはきちんと証明できるべきでしょう。これも背理法による証明です。以下に証明を書いておきますので、何も見ずともすらすら書けるようにしておきましょう。

類題を解いてみよう

　以上、「日本の大学入試史上最も短い数学の問題」を紹介しました。ですが、もっと短い問題もこの世には存在します。今回はそのような「とても短い問題」をあと2題紹介します。

第1問：ax=bを解け。

　これは筆者が昔お世話になった数学の先生がよく出題していた問題です。「このようなものは中学生でも解けるのでは？」って思われるかもしれませんが、果たしてどうでしょう？解答はこちらです。

　どうでしょう？x=b/aだけ書いて満足してはいけませんよ。aが0でない場合でしかそれは成立しません。実際に解答を書き始める前に立ち止まる必要があることを教えてくれるいい問題です。どこかの大学入試にもこれから出現するかもしれません。

第2問：3^√3は整数か？

　2022年の春先に「5^πは整数か？」という問題が現れました。実際の大学入試の問題ではないのですが、「京大の問題より短い！」ということで一部では結構話題になったようです。この問題は高校数学の範囲内で解くのは厳しいので、見出しに示した問題で代用します。

　√3の概数値が1.7320508……となることは知っているかと思います。今回はこれを用いて解きますが、この事実をそのまま使ったところで解けるものでもありません。一工夫要ります。それは、√3をこの値に近い有理数ではさみ、3^√3が整数となりえないことを大小比較で示すことです。

　こうしてみれば中学生でも解けそうなほど簡単な問題です。しかしこれだけ問題文が短いと、そこからどうやって解答に辿り着けばよいのか、ビジョンが浮かばないかもしれません。それでも「3^√3が整数だと仮定すればおかしいことを示す」という基本方針は変わりません。臆せずにいきましょう。

　1<√3<2であることから「もし整数なら4,5,6,7,8のどれかになるだろう」と考えてから解き始めてここまでしぼるのがよさそうです。この一題だけで記事を書けそうなほどいい問題ではありますが、これは架空の入試問題です。本番でこれが出題されたら幸運程度に考えてください。

実際の大学入試本番で
合格点を取るためには？

　以上3題、「極端に短い数学の問題」を見ていただきました。ですが、このような問題は一般には「捨て問」となります。ほとんどの場合は、問題文中のヒントがあまりに少ないものは無視し、他の簡単なものを解くことになります。

　ではなぜ今回ここで解いたのか？と思われるかもしれません。それはひとえに大学入試、そして数学という科目の本番には魔物が棲んでいるためです。今回のtan1°の問題が出題された京都大学でも、直近では2020年度入試は受験生のトラウマになるほど恐ろしいものでした。

　まれに「一題たりとも基本問題が存在しない」出題セットが出現し、簡単な問題で点を稼ごうとする作戦が通用しない年があります。もし本番でそのような事態が起きたらどうするか、それを想定した対策を立てねばなりません。「大失敗しても受かる」ようにする必要があります。

　そのためにはひたすら問題を解いていくしかありません。数学が難しい場合は他教科でカバーするのが鉄則ですが、それでも合格ライン付近は熾烈な争いです。この争いに打ち勝つためにも、数学で1点でも多く取れるよう日々努力する必要があります。

　しかし、そのための努力は容易なものではありません。数学などどうせギャンブルなのだから、こんな教科のために労力を費やしたくないと考えてしまうのも自然なことです。それに、どうせ入試に向けた数学の勉強をするなら、苦しまない、楽しい方法で実力を伸ばしたいところです。

　そのようなお悩みを解決できるのが東大家庭教師友の会所属の学生家庭教師です。彼らは数学の指導に優れるだけでなく、お兄さんお姉さん感覚で接することができるので、日々楽しく実力をつけることができます。悩み事がある場合も、積極的に相談に乗ってくれます。

　大学入試の数学を攻略したい、第一志望校に合格したいあなたの背中を、私達東大家庭教師友の会は全力で押します。