東京工業大学の数学の良問その１　～答えはすぐに分かるけれど～

この問題を解くために
必要な考え方

　まずはこうしたnが現れる問題の攻略法を確認します。今回は難しそうなので、「小さいnを具体的に代入して試す」ということをやってみましょう。実際、これをやってみると、a_1=19^1+2^1=21、a_2=19^2-2^5=361-32=329と出てきます。そして、この両者を割り切る素数を調べると、これが7しかないことが即座にわかります。

　すべてのnに対してa_nを割り切るにあたってはn=1,n=2に対しても割り切れていなければならないですから、この時点で求めるべき素数が7であることが確定します。これは「必要条件でしぼる」という方法です。他の問題にもそのまま使えるので覚えておきましょう。ですが、これだけで「答えは7」と書いた場合、あなたの得点は0点です。

　そもそも問題文には「すべてのnに対して」とあります。まだn=1とn=2の場合しか調べていません。一般的なnに対してa_nが7で割り切れることを示す必要があります。なので、この問題は「すべてのnに対してa_nは7で割り切れることを証明する」問題であると読み替えられます。

　ただ、ここからが本番です。この問題には主に「二項変形によってa_nを7の倍数の形で表現する」「漸化式を作り、数学的帰納法によって証明する」の2通りの解法が存在します。どちらもかなり解答に起こすまでに手間がかかる解法です。ここからは実際の解答をお見せしつつ、どのように解答を作成すればよいかを解説します。

二項変形による解答の作り方

　そもそも「二項変形ってなんだ…？」となっている読者の方もいるかもしれません。問題文中にある19^nで説明します。19と7に対してユークリッドの互除法を使うと、19=7・2+5となりますから、これを用いて19^n=(7・2+5)^nと書き換えます。こうすると二項定理が使えるようになります。このように、何らかのn乗になる数を二項定理が使える形に変形するのが二項変形です。

　二項定理をそもそも忘れている方は数学Ⅱの教科書をもう一度読み直しましょう。この二項変形を利用することにより、例えば以下のような解答を書くことができます。ただこの解法は少し上級者向けです。出来れば簡単なのですが、整数問題が苦手な人は一度この節を読み飛ばし、数学的帰納法の方の解説を読まれることをお勧めします。

 

　19が21(=7×3)より2小さい数であることと16が14(=7×2)より2大きいことが上手く噛み合っています。また、19=35-16であることを利用すると、さらに解答を短くできます。実際に見てみましょう。

 

　これは少し思いつきにくいかもしれません。これだけ難しい問題にしては解答が短いですがこれで満点です。数学的には全て正しく、なおかつ過不足もありません。不安であれば二項定理の変形をもう少し詳しく記す程度はやっていいかもしれません。

　見た目も美しく、流れるようにきれいな解答ですがこの解答に至るには発想が必要になる部分が多いです。ですが、発想は偶然の産物では決してありません。ここからは解答を書くなかで「必然的に」発想ができるようになる具体的なやり方を伝授します。

　まずはa_nの式を解答にあるように書き直しましょう。2の4n乗のままでは扱いにくいです。a_nが7の倍数であることを示したいのですから、ある程度は見通しが立つ形にする必要があります。今回の変形はやや骨が折れる形ですので、変形の仕方の正解を書きます。

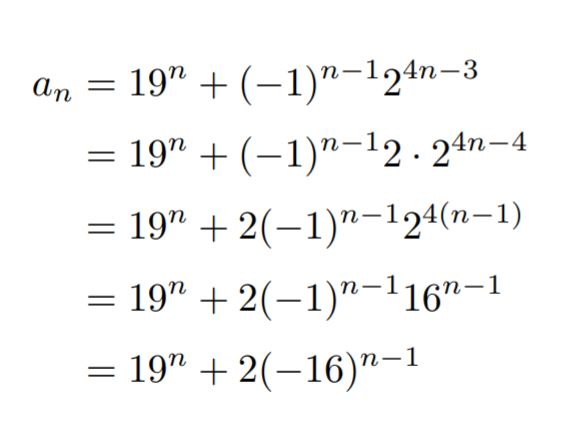
　4n-3乗を4(n-1)+1乗と見るのがミソです。結局この2つの項で足したり引いたりをすることになりますから、それぞれのべき数をある程度揃えておくのが大切になります。

　このように変形できたら、次はどのように二項変形を施すかを考えます。今回の二項変形は①7の倍数になる部分を取り出して②7の倍数にならない部分を足し算で相殺することを目的にしていますから、上に書いたような変形をするわけです。

　こうした「〇〇を示す問題」を考える際に意識してほしいことは「結論から逆算する」ことです。今回は7の倍数であることを示したいわけですから、7の倍数になるような式変形が必要になる、ということを常に頭に入れましょう。そうでなければドツボにハマります。

　また、「これ以上計算できないと思ったら他の変形を考える」ことも重要です。例えば、19=7・2+5と変形してしまうかもしれません。こうなると結論に辿り着くのが難しくなります。先が見えなくなった、と感じたらすぐに別のやり方を考えましょう。

　整数問題では特にこのような方針変更を柔軟にやっていく必要があります。筆を動かすことなく唸って、ただ時間だけが過ぎていく。本番ではこうなってはなりません。問題そのものが難しいと判断したら、先に他の問題を解きに行くことも大事でしょう。

数学的帰納法による
解答の作り方

　次に数学的帰納法による解答を書きます。二項変形による作り方がイマイチ理解できていない、という方でもこちらはわかるかと思います。ただし、前項にあった2^4n=16^nの変形は使用しています。

 

　こちらも解答そのものは綺麗だけど発想がやや難しい、というパターンです。１つこれは知識として入れておいて欲しいのですが、「全てのa_nについて示す問題は帰納法と漸化式を両方使う」と覚えておいてください。恐らく帰納法自体の初出が漸化式の直後だと思いますので、これで認識している人も多いかと思います。

　ここまで来れたらあとは漸化式を作ればよいのですが、ここで一ひねりいります。①a_n+1とa_nをつなげられる式であり、なおかつ②a_n+1が7の倍数であることを示せる漸化式を用意しなければならないからです。そこで、19と16を足したら35になることに注目して変形を行うのですが、この変形もやや骨が折れます。

　逆に、この変形が出来るならあとは何も難しくありません。変形で詰まったら、「そもそも何のために変形をしようとしているのか」を思い出してください。7の倍数にしたい、これを念頭に置いて式をもう一度見つめることが大事になります。

実際に本番の整数問題が
解けるようになるには？

　今回取り上げた問題はかなり難しい問題だったと思います。やり方は分かっても、その先の細かいテクニックがわからなくて解答を仕上げられない、そういうモヤモヤとの戦いだったのではないでしょうか？ここからはそんな「難しい」整数問題の解法について説明します。

　整数問題は大きく分けて3つの作戦を取って戦うことになります。1つは「剰余類で分ける」、1つは「二項定理を用いる」、そしてもう1つは「帰納法を使う」です。今回はそのうち二項定理と帰納法を使った解法を解説しました。一応、剰余類による解法もあるのですがそれは今回の場合あまりに解答を長くする悪手だったので省略しました。

　話を戻すと、整数問題の基本方針は上の3つしかありません。他の解法を使わなければいけない問題がもしあっても、その問題は誰も触りたがらない難問であるはずなので無視してよいです。とにかく、整数問題が出たら上の3つのうちどれがいいかを考えてから解答を組み始めるようにしましょう。

　そして、「難しい」整数問題というのは上の3つのどれをとっても今回のように変形で詰まる、そもそも解答が長くなりすぎるといった問題が立ち塞がります。今回は練習のためあえて解いて頂きましたが、本番では他の問題の難易度と他教科の得点との兼ね合い次第では無視してよいです。

　ですが、このような問題が基本問題にプラスして取れる、という場合は合格が一気に近付きます。ではどうやって取るのか、というとこれには「整数問題そのものに慣れる」ことしかないのが実情です。

　難関大学は好んで整数問題を出します。これはよく「閃きがするどい受験生を取りたい」という思惑が働いているため、と説明されますがそれだけではないでしょう。発想は十分なインプットなしにはあり得ません。ここで必要なインプットは整数問題を数多く解くことです。

　しかし、だからといってやみくもに問題を解き続けていればよいのかというとそうでもありません。世の中の入試問題は玉石混交です。数学の他の分野と、それに他教科の勉強もしなければならないことを考えれば、多くの問題を解くべきだけど、ある程度は絞った方が良いというジレンマがあるのです。

　この匙加減の問題を1人で解決するのは難しいです。そこで、こうした個々人の受験スタイルをサポートしてくれる人として大変優秀な、東大家庭教師友の会所属の家庭教師をご紹介します。

　友の会所属の家庭教師の強みは全員が難関大在籍の現役学生家庭教師であることです。彼らは実際に難関大の整数問題、そして数学を攻略するためのノウハウを持っているだけでなく、大学受験を経験して日が浅いことから、親身になってあなたのサポートをすることができます。

　また、全員が通過率20%以下の厳しい審査を通っています。このため、生徒様のサポートを卒なくこなせる学力だけでなく、立派な人格まで備えた家庭教師をご紹介することが出来ます。大学入試の数学を攻略したい、第一志望校に合格したいというあなたの背中を、私達友の会は全力で押します！