東京工業大学の数学の良問その２　～複素数平面、基本のキ～

複素数平面の攻略に
必要な考え方

　理系の人は数学Cで複素数平面を学ぶのですが、実際にやってみてどうでしょうか？やることが多くて難しい、と感じたのではないでしょうか？実際その直感は正しいです。複素数平面の問題を解くためにはいくつもの他分野の知識や手法が必要になります。

　まず最初に認識していただきたいことは「複素数平面≒ベクトル平面である」ということです。例えば、複素数平面上の点2+iは原点から伸びるベクトル(2,1)とまったく同じです。x軸方向の単位ベクトルを1、y軸方向の単位ベクトルをiと書くことで、ベクトル平面を複素数平面に書き換えられる、といった具合です。

　このことを用いれば複素数を図形的に考えられるようになります。純粋な幾何の問題をベクトルで考えると簡単に解決できる場合があるのと同様、普通に数式を計算すると大変な問題もシンプルにすることができます。

　また、極座標を同じく数学Cで習ったかと思います。複素数は極座標での表現が可能です。先ほど例に挙げた2+iも、√5(cos30°+isin30°)と書き換えることで、(r,θ)=(√5, 30°)と同じになることがわかります。

　さらに複素数には特有の性質があります。複素数z=x+yiに対し、x-yiは共役な複素数と呼ばれ、zの上にバーを付けて表されます。そして、複素数zに対する方程式f(z)=0が複素数αを解に持つ場合、それに共役な複素数も解に含まれます。

　ここまでの特徴を知っていれば理論上は複素数平面の問題が解けます。しかし知っているだけではまだ足りません。どのような時にどのルールを適用すれば解けるかまで把握しておかなければ、実際の問題には手も足も出ないでしょう。ここからは実際に問題を解く方法を解説します。

　複素数平面の問題を解くための方法は大きく分けて「z=x+yiと置き換える」「z=cosθ+isinθにする」「複素共役を用いる」「図形的に考える」の4択です。早速質問ですが、今回はどのようにすれば解けるでしょうか？考えてみてください。

今回の問題を解くために
必要な考え方

　それでは先ほどの質問の正解を発表します。答えは「z=x+yiまたはz=cosθ+isinθの置き換えと複素共役を両方使う」です。このように複素数平面の分野では上に挙げた方法を複数用いて問題を解くことが多いです。

　今回の問題でいえば、3次方程式x^3-x+k=0が与えられているので、まずはこれの解をα、β、γとおきます。さらに、実数でない複素数αに対して、βは共役であるとし、さらにγは実数であるとします。先ほど解説した性質をそのまま活用します。

　ここで「いきなりγを実数とおいていいのか？」と思われたかもしれませんが、良いのです。実数全体は複素数全体に含まれます。そして、任意の実数に対して共役な複素数はその実数それ自体になります。これにより、γを実数とすることができます。

　次はαとβの表し方を考えます。ここで解法は2つに分岐します。1つはα=x+yi、β=x-yiとするパターン、もう1つはα=cosθ+isinθ、β=cosθ-isinθとおくパターンです。どちらの解法でも問題なく正答することができます。それでは解答をお見せします。

解答

　まず、α=a+biとおいて作った解答がこちらになります。

 

次に、α=cosθ+isinθとした場合の解答を掲載します。

 

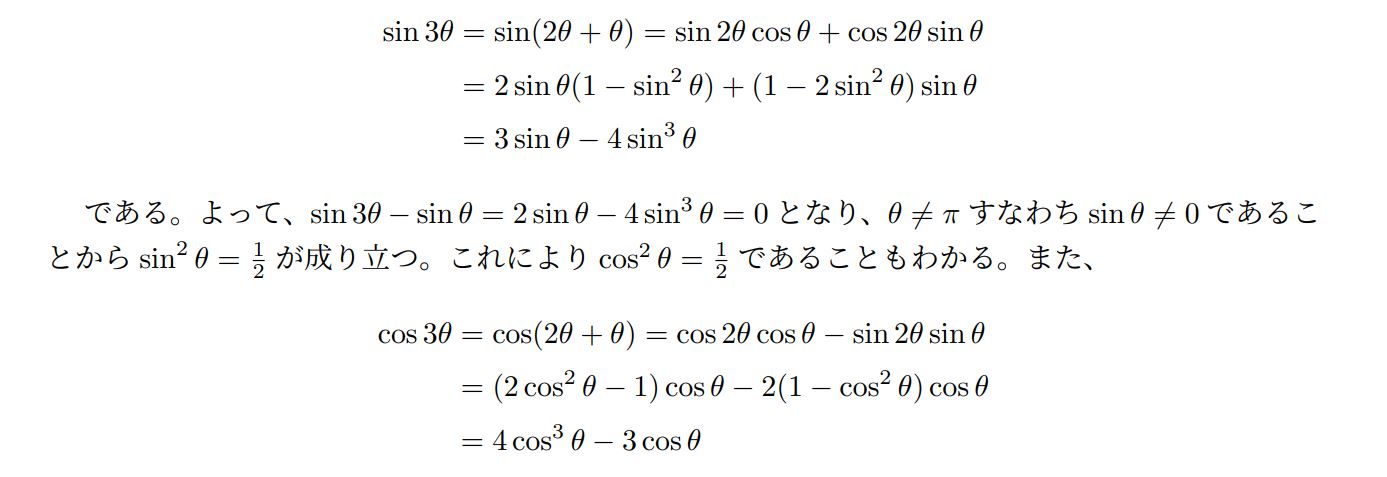
　このような解答が書ければ完璧であると思われます。k>0によって条件をしぼるとkの値が確定するのでこれも利用することになります。最後の実数解は片っ端から代入して見つけて構いません。実数の解が1つしかないことは予め分かっているからです。

　極形式を利用する解答でド・モアブルの定理を使用する際は、必ず定理の名前を書きましょう。書かなければ減点の恐れがあります。また、解答中で3倍角の導出を行う必要はありませんが、3倍角の公式は丸暗記しない方がよいです。加法定理と倍角の定理から毎回導くようにすることをお勧めします。

　今回はかなり簡単な問題を選出しましたが、複素数平面の問題をほとんど解いたことがない場合はこれでも難しいと思います。慣れが重要な分野ですので、様々な問題に触れ、多彩な解き方を身につけていくことをお勧めします。

数学Cの問題を
解けるようにするために

　以上、複素数平面の問題を解いて頂きました。簡単な問題ではありますが、あまり経験がなく、かなり苦労した人もいたのではないでしょうか。

　2022年度の教育課程より復活した数学Cには主に「ベクトル」「極形式」「複素数平面」「行列」の4つの単元が含まれます。微積・極限で計算地獄の数学Ⅲとは打って変わって、こちらは複雑な計算はあまり要しません。しかしその分、癖の強いトリッキーな分野が揃っています。

　その代表格が複素数平面、というわけです。複素数平面という分野は大学の数学でいえば、主に「線形代数」「ベクトル解析」「複素関数論」「平面幾何学」の4分野に跨ります。そのため教科書などの記述もまとまりを得づらく、初見の生徒様には難しい分野であるといえます。

　東大家庭教師友の会では複素数平面に強い家庭教師を紹介できます。彼らは現役で東工大や京大、東大といった難関大学に在籍しており、高い数学の指導力を有しています。彼らをパートナーにできれば、複素数平面のようなトリッキーな分野も怖くないでしょう。

　しかし、それは「きちんと手を動かせて」の話です。いくら彼らの指導力が高いとはいえ、生徒様ご自身が自らの手で問題を解くことをしなければ、数学の学力は向上しません。そうなっては、家庭教師を雇う意味などない……そう考えられるかもしれません。

　しかし、東大家庭教師友の会の教師であればそのような心配はありません。彼らはモチベーション管理やメンタルケアにおいても卓越しているからです。生徒様と二人三脚で高校の数学を攻略し、第一志望の合格に向けて邁進します。

　大学入試の数学を攻略したい、第一志望校に合格したいあなたの背中を、私達東大家庭教師友の会は全力で押します。