ほとんどの受験生は
こういう間違いをした!
問題文をぱっと見ただけでは「これが本当に誰も解けなかった難問なのか?」と思われるでしょう。では一体どのあたりが難しいのかを調べるために実際に解いてみましょう。当時、ほとんどの受験生は以下のような解答を書きました。
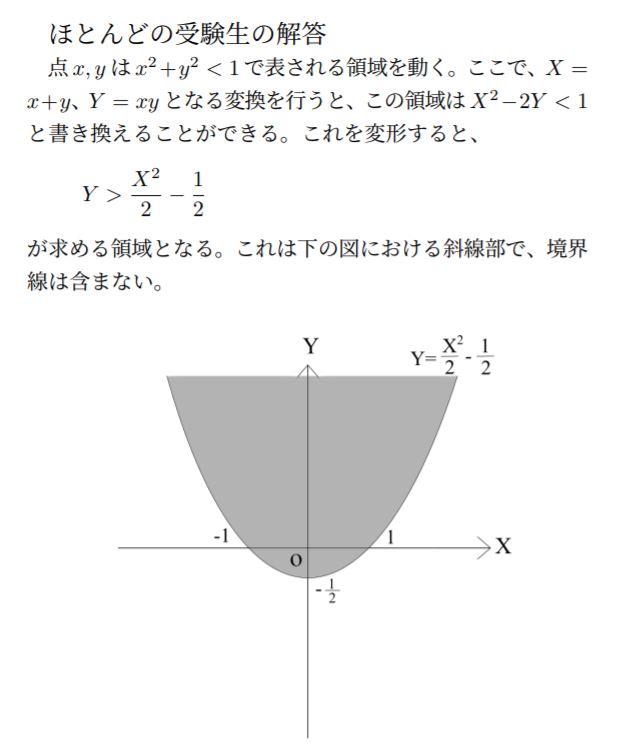
一見してどこもおかしいところはないように思えます。しかし、この解答は不正解です。部分点は20点中の5点取れればラッキー、というぐらいでしょう。この解答にはある「モノ」が不足しています。ここからはその不足しているモノが何なのか、ということを見ていきます。
この問題を解くために
必要な考え方
この問題に必要なやり方は「逆像法」と一般に呼ばれる手法です(逆手流という言い方もあります)。ですが、逆像法とは何なのか、という説明をしようとすると「写像」と呼ばれる大学で習う本格的な数学の知識が必要になりますので、これについて、まずはかなり噛み砕いた説明をすることにします。
まず皆さんに最初に考えて欲しいことがあります。$$x+y=4とxy=10を満たす実数の組(x,y)$$ 以上のものが果たして存在するか?ということです。早速調べてみましょう。まずは左側の式を変形して右側の式に代入しましょう。すると、$$x(4-x)=10$$という形になると思います。これはxについての2次方程式ですから、この解を求めてみましょう。すると、$$x=2+sqrt{6}i, 2-sqrt{6}i$$という結果になります。そうです、X=4とY=10を満たす実数xとyの組は存在できないのです。
こうした変数変換を伴う問題にはしばしばこのような落とし穴があります。つまり、このような問題を見かけたら「元の変数が満たすべき要件をしっかりと満たせるか」ということに常に注意しながら解かねばならない、ということなのです。そして、その要件を満たす条件を、今回の問題で言えば(x,y)が実数になる条件を求めるために、逆像法の考え方が必要なのです。
逆像法について
いよいよ逆像法の概要を説明します。やや難解な説明ですが、今回の問題の解き方を理解するには必要な作業なので、苦手な方も頑張って解読してみてください。
まず集合AとBを考え、(x,y)と(X,Y)をそれぞれ集合Aと集合Bに属する実数の組であるとします。今回の問題では集合Aが半径1の円の内部に、集合Bがこれから図示するべき領域に該当します。
一般的な解析(計算)手法(これはしばしば逆像法と対比して「順像法」とよばれます)は、(x,y)を先に考え、これを所定の手続きで(X,Y)に変換するという、先ほど示した誤答で使用したステップを踏みます。もちろんこれも今回の解答を得るために必要なステップです。ですが、それだけでは不足し、前節に取り上げたような問題が起こります。
これを解消するために、今度は(X,Y)が存在できる条件を満たす(x,y)を探す、という方針を取ります。これが逆像法です。ランダムにXとYの値を考え、これを満たす(x,y)が実数となるものを探します。高校の段階で使える、元の変数が実数かどうかを調べる方法といえば判別式です。
先ほどはx^2-4x+10=0という2次方程式を解きました。これを一般のXとYを含む方程式にすることになります。「yについては考えなくてもよいのか?」と思われるかもしれませんが、xとXの値が実数で与えられればyの値も必ず実数で与えられるため、それは不要である、ということになります。もちろん、yについての2次方程式としても構いません。対称性から同じ結果を得られます。
とりあえず、以上の考察から今回逆像法によって元のxとyを実数にするための方法は、xについての2次方程式$$x^2-Xx+Y=0$$ の判別式Dが0以上になる(X,Y)の範囲を求めることである、ということがわかりました。それでは解答を書きます。
解答

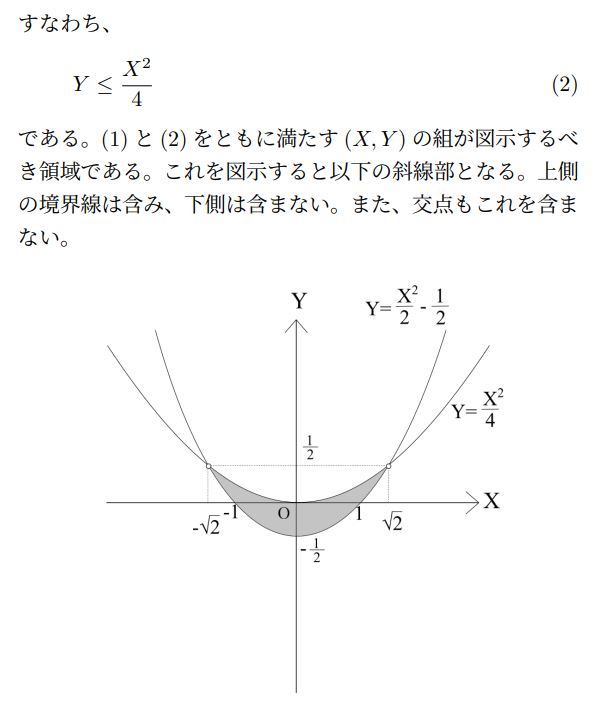
以上のような領域が出てくれば正解となります。この領域の図がまるで赤門に座す閻魔大王の微笑に見えることから、このタイプの問題は「閻魔の唇問題」とよばれています。
注意点としては図示の際に文面で領域についての補足説明をしっかりと行うことです。特に今回は含むべき境界線と含むべきではない境界線が混在するため、このあたりをしっかりと説明しないと減点必至です。最後までしっかりと合わせましょう。
大学入試の数学の問題を
解けるようにするために
以上に見た「逆像法」ですが、一般の高校の数学の教科書には載っていません。「東大の問題は理論上教科書の知識だけで解ける」と比較ページでは説明したのですが、これは半分嘘です。もしこれが真であるとすればどこの大学の問題も教科書の勉強だけで満点が取れます。
難関大学の数学の入試問題はこのような「教科書に載っていないこと」であふれています。今回の逆像法の問題も知らなければほぼ解けません。だからこそ、この問題は「典型問題」として今なお教育現場で取り上げられ続けているのです。
すると、大学入試の数学を攻略するためにはさまざまな種類の問題を解いていかなければならない、ということに必然的に気が付くはずです。特に理系の場合、難関大学に受かろうと思えば目安として1日に5時間以上は数学につぎ込み、数多くの出題パターンに慣れていかなければなりません。
上のような地道な鍛錬をせずに合格するような人はごく一部です。それ以外の人は努力なしにはどうしようもありません。ですがその努力をすることも容易ではありません。合格するその日まで耐え忍ぶだけの我慢強さがある人もほんの一握りです。
このような現実を見れば、もうどうしようもない、自分はもう受かりようがないと考えてしまうかもしれません。ですが、これは全て「たった一人でやっていれば」の話です。一緒に夢を追いかけられる人がいれば、合格までのハードルは大きく下がります。
その「一緒に夢を追いかける人」として最適なのが東大家庭教師友の会が紹介する学生家庭教師です。彼らは大学受験を数年前に経験したばかりなので当時の感覚を覚えており、社会人の家庭教師と比べて、より共感と思いやりをもって生徒様へのメンタルケアを行うことができます。
また、彼らは全員東大・京大・東工大をはじめとする難関大学に所属しており、家庭教師として求められる高校数学のノウハウもしっかり会得しています。大学入試の数学を攻略したい、第一志望校に合格したいというあなたの背中を、東大家庭教師友の会は全力で押します。
あわせて読みたい|大学数学の良問を解説!
東大家庭教師友の会の特徴
当会には、東大生約9,700名、早稲田大学生約8,500名、慶應大生約8,000名をはじめ、現役難関大生が在籍しています。
生徒様の憧れとなる教師のご紹介と、安心・充実のサポート体制で、生徒様の目標達成に貢献します。
大学受験数学の指導ができる家庭教師の紹介
上記は在籍教師の一例です。他にも様々な経歴の教師が在籍しています。ご希望の条件の教師が在籍しているかは無料でお探しできますので、まずはお気軽にお問合せください。
オンラインでの指導も可能です
東大家庭教師友の会オンラインHPを見る



















